复盘｜Acwing第88场周赛

【Acwing 周赛复盘】第88场周赛复盘（2023.1.28）

周赛复盘 ✍️

本周个人排名：894/2025

AC情况：1/3

周赛当天晚上，博主在影院观看《流浪地球2》，未实时参加，是在之后的时间里定时自测的。🎬

感觉自测的氛围和实时比赛还是很不一样的，没有比赛时那种紧张感。人比较松弛，解题时相对从容淡定，希望真正比赛时，也能保持这样的心态，而不是无谓的焦急和紧张。😊

这也是博主参加的第三次周赛，经过前两次的历练，感觉自己的水平已经有一点提升了。虽然从纸面数据来看，这次只 AC 了 1 题，但是自己做题时的思路却相比前两次开阔了不少，代码完成度也比较高。

T2 博主是用邻接表存储图，然后对于每个点 DFS 搜索，最后通过邻接矩阵判断所有点是否互通（现场提交时一直 Segmentation Fault，没能顺利找出 BUG。复盘时，顺利找出相关BUG（还挺多的。。。），最终根据该思路写出相应 AC 代码；当然，经过y总讲解，发现本题也是一道 思维题，直接判断最外层是否为 顺时针/逆时针 即可。

T3 博主第一反应是用DP，根据思路写出了大部分代码，但是提交结果是 11/15，仍有 4 个测试点没有通过。复盘时，经过y总讲解，去学习了 状态机DP 的相关内容，顺利写出AC代码。

总之来说，周赛给自己的提升还是很大的，继续加油 😀

周赛信息 📚

时间：2023年 1 月 28 日 19：00-20：15

竞赛链接：https://www.acwing.com/activity/content/2840/

y总直播间：http://live.bilibili.com/21871779

y总录播讲解视频：【AcWing杯 - 第 88 场周赛讲解】

题目列表 🧑🏻‍💻

题目名称	原题链接	视频链接	难度
4800. 下一个	原题链接	视频链接	简单 🟢
4801. 强连通图	原题链接	视频链接	中等 🟡
4802. 金明的假期	原题链接	视频链接	中等 🟡

---

题解 🚀

【题目A】下一个

【题目描述】

给定一个整数 $x$，请你找到严格大于 $x$ 且各位数字均不相同的最小整数 $y$。

【输入】

一个整数 $x$。

【输出】

一个整数 $y$。

保证一定有解。

【数据范围】

所有测试点满足 $1000 \le x \le 9000$。

【输入样例1】

1987

【输出样例1】

2013

【输入样例2】

2013

【输出样例2】

2014

【原题链接】

https://www.acwing.com/problem/content/4803/

---

【题目分析】

签到题，简单枚举 + 判断即可，判断是否重复的方式有很多种，如：

• 利用 to_string 将数字转换成字符串 -> 利用 set 自动去重 -> 比较两个字符串的长度
• 利用 数字分割 + 桶 的方式，判断重复

【复盘后的优化代码】✅

#include<bits/stdc++.h>

using namespace std;

int main() {
    int x;
    cin >> x;
    for (int i = x + 1;; i++) {
        // 将当前数字i转换成字符串
        string str = to_string(i);

        // set自带去重功能，判断两个字符串长度是否一致，即可判断数字是否重复
        set<char> str2(str.begin(), str.end());
        if (str.length() == str2.size()) {
            cout << i << endl;
            break;
        }
    }

    return 0;
}

【周赛现场 AC 代码】

#include<bits/stdc++.h>

using namespace std;
const int N = 15;

int x, b[N];

// 判断当前数字t的各个位数是否不同，采用桶的思想
bool check(int t) {
    while (t > 0) {
        if (++b[t % 10] > 1) return false;
        else t = t / 10;
    }
    return true;
}

int main() {

    cin >> x;
    int t = x + 1;
    while (1) {
        // 判断当前t是否满足条件
        if (check(t)) {
            cout << t << endl;
            break;
        } else {
            t++;
            memset(b, 0, sizeof b);
        }
    }

    return 0;
}

---

【题目B】4801. 强连通图

【题目描述】

给定一个平面。

平面中有 $n$ 条与 $x$ 轴平行的 有向边，从上到下依次编号为 $1∼n$，每条边都无限长，且两两不重合。

平面中有 $m$ 条与 $y$ 轴平行的 有向边，从左到右依次编号为 $1∼m$，每条边都无限长，且两两不重合。

这些边一共有 $n×m$ 个交点。

给定每条边的具体方向，请你判断这 $n×m$ 个交点是否满足：从任意交点出发可以到达任意其它交点。

【输入】

第一行包含两个整数 $n,m$。

第二行包含一个长度为 $n$，由 < 和 > 构成的字符串，其中第 $i$ 个字符用来表示第 $i$ 条与 $x$ 轴平行的 有向边 的方向，如果为 < 表示方向从右向左，如果为 > 表示方向从左向右。

第三行包含一个长度为 $m$，由 ^ 和 v 构成的字符串，其中第 $i$ 个字符用来表示第 $i$ 条与 $y$ 轴平行的 有向边 的方向，如果为 ^ 表示方向从下向上，如果为 v 表示方向从上向下。

【输出】

如果所有交点满足题目要求，则输出 YES，否则输出 NO。

【数据范围】

前 $5$ 个测试点满足 $2 \le n,m \le 6$。

所有测试点满足 $2 \le n,m \le 20$。

【输入样例1】

3 3
><>
v^v

【输出样例1】

NO

【输入样例2】

4 6
<><>
v^v^v^

【输出样例2】

YES

【原题链接】

https://www.acwing.com/problem/content/4804/

---

【题目分析】

本题是一道隐藏较深的思维题。

在该题目背景下，想要证明所有点互通，只需要判断 四个角落上的点 是否互通 / 四条外边是否为逆时针、顺时针 即可。具体讲解见y总视频：视频链接

简单理解：该条件下，任意点A可以通过其所在的直线走到最外圈，然后还能再回到原来的位置，而其他任意点B也可以通过先到最外圈，再到点A的方式与A连通，因此所有点都是互通的。

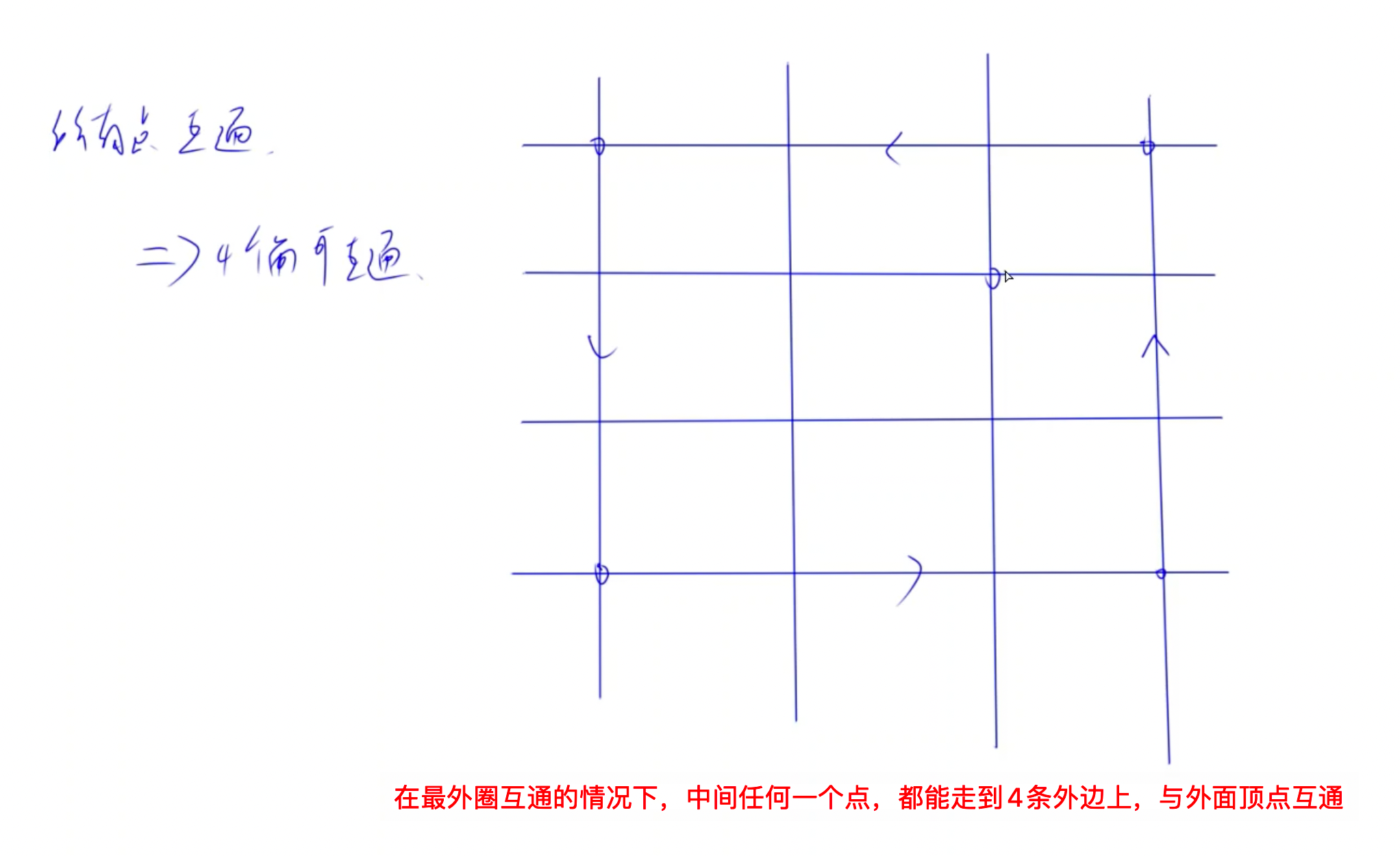
当然，本题也可以用 DFS/BFS + 图论的知识来解决，但是相应代码较为繁琐，BUG修改起来比较麻烦。（博主本人在复盘时改了好久的周赛现场代码，才顺利AC 😂）

【复盘后的优化代码】（思维题）✅

#include<bits/stdc++.h>

using namespace std;
int n, m;
string str;
char a, b, c, d; // 代表四条边

int main() {
    cin >> n >> m;

    // 顶边和底边
    cin >> str;
    a = str[0], c = str.back();

    // 左边和右边
    cin >> str;
    b = str.back(), d = str[0];

    // 判断顺时针 / 逆时针
    if ((a == '>' && b == 'v' && c == '<' && d == '^') || a == '<' && b == '^' && c == '>' && d == 'v') {
        cout << "YES" << endl;
    } else {
        cout << "NO" << endl;
    }

    return 0;
}

【复盘后的周赛现场代码】（邻接表 + DFS + 邻接矩阵判断）✅

#include<bits/stdc++.h>

using namespace std;
const int N = 410, M = N * 2;
int h[N], e[M], ne[M], idx;
bool st[N][N];
int n, m, sum;
char c;

void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

// 对于每一条水平线，横向加 m-1 条有向边
void inputH() {
    // 共有n条水平线，读入n个符号
    for (int i = 1; i <= n; ++i) {
        cin >> c;
        // 水平线方向"->"
        // add(1,2),add(2,3)...add(m-1,m) 第1条水平线
        // add((i-1)*m+1,(i-1)*m+2),add((i-1)*m+2,(i-1)*m+3),...add((i-1)*m+m-1,(i-1)*m+m) 第i条水平线
        if (c == '>') {
            for (int j = 1; j < m; ++j) {
                add((i - 1) * m + j, (i - 1) * m + j + 1);
            }

        // 水平线方向"<-"，同理，注意下标计算有变化
        } else if (c == '<') {
            for (int j = m; j > 1; --j) {
                add((i - 1) * m + j, (i - 1) * m + j - 1);
            }
        }
    }
}

// 对于每一条垂直线，纵向加 n-1 条有向边
void inputV() {
    // 共有m条垂直线，读入m个符号
    for (int i = 1; i <= m; ++i) {
        cin >> c;
        // 垂直线方向"v"（以m=3,n=3为例）
        // add(1,4),add(4,7) 第1条垂直线
        // add(2,5),add(5,8) 第2条垂直线
        // add(i,m+i),add(m+i,2*m+i),... 第i条垂直线
        if (c == 'v') {
            for (int j = 1; j < n; ++j) {
                add((j - 1) * m + i, j * m + i);
            }

        // 水平线方向"<-"，同理，注意下标计算有变化
        } else if (c == '^') {
            for (int j = n; j > 1; --j) {
                add((j - 1) * m + i, (j - 2) * m + i);
            }
        }
    }
}

// 深度优先搜索，遍历当前结点u的邻接表
void dfs(int u, int chi) {
    for (int i = h[chi]; ~i; i = ne[i]) {
        int j = e[i];
        // 防止死循环，往回搜索
        if (st[u][j]) {
            continue;
        }
        st[u][j] = true;
        dfs(u, j);
    }
}

int main() {
    ios::sync_with_stdio(false);  //cin读入优化
    cin.tie(0);

    cin >> n >> m;
    sum = n * m;  // 顶点总数

    // 加边
    memset(h, -1, sizeof h);
    inputH(); // 横向加边
    inputV(); // 纵向加边

    // dfs搜索，判断每一个点是否能够到达其他所有点，结果存储在邻接矩阵st中
    for (int i = 1; i <= sum; ++i) {
        // 本身默认可到达，即对角线设置为1
        st[i][i] = true;
        dfs(i, i);
    }

    // 判断邻接矩阵值是否均为1，若都是1，表示所有点互通
    bool flag = true;
    for (int i = 1; i <= sum; ++i) {
        for (int j = 1; j <= sum; ++j) {
            if (!st[i][j]) {
                flag = false;
                goto end;
            }
        }
    }
    end:
    if (flag) cout << "YES" << endl;
    else cout << "NO" << endl;

    return 0;
}

【周赛现场未 AC 代码】（下面的代码有不少BUG，是不错的反面案例）❌

#include<bits/stdc++.h>

using namespace std;
const int N = 10000, M = 10000;
int h[N], e[M], ne[M], idx;
bool st[N][N];
int n, m, sum;
char c;

void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void dfs(int u, int chi) {

    for (int i = h[chi]; ~i; i = ne[i]) {
        int j = e[i];
        st[u][j] = true;
        dfs(u, j);
    }

}

int main() {
    ios::sync_with_stdio(false);  //cin读入优化
    cin.tie(0);

    cin >> n >> m;
    sum = n * m;
    memset(h, -1, sizeof h);
    for (int i = 1; i <= n; ++i) {
        cin >> c;
        if (c == '>') {
            for (int j = 1; j < n; ++j) {
                add((i - 1) * n + j, (i - 1) * n + j + 1);
            }
        } else if (c == '<') {
            for (int j = n; j > 1; ++j) {
                add((i - 1) * n + j, (i - 1) * n + j - 1);
            }
        }
    }

    for (int i = 1; i <= m; ++i) {
        cin >> c;
        if (c == '^') {
            for (int j = 1; j < n; ++j) {
                add((j - 1) * n + 1, j * n + 1);
            }
        } else if (c == 'v') {
            for (int j = n; j > 1; ++j) {
                add((j - 1) * n + 1, (j - 2) * n + 1);
            }
        }
    }

    for (int i = 1; i <= sum; ++i) {
        dfs(i, i);
    }

    bool flag = true;
    for (int i = 1; i <= sum; ++i) {
        for (int j = 1; j <= sum; ++j) {
            if (!st[i][j]) {
                flag = false;
                goto end;
            }
        }
    }
    end:
    if (flag) cout << "YES" << endl;
    else cout << "NO" << endl;

    return 0;
}

【代码对比总结】

经过复盘后的仔细修改，可以发现周赛现场未 AC 的代码有不少BUG，如 死循环、下标计算错误导致越界、for循环条件书写错误（如 j-- 写成了 j++）等，这些都是之后在书写代码时，需要注意的。☘️

---

【题目C】金明的假期

【题目描述】

金明有 $n$ 天假期，编号 $1∼n$。

整个假期期间，他每天只可能有三种选择：

1. 去健身房健身一整天。（前提是当天健身房开放）
2. 去图书馆看书一整天。（前提是当天图书馆开放）
3. 在家休息一整天。

用一个长度为 $n$ 的整数数组 $a_1,a_2,\dots,a_n$ 来表示这 $n$ 天健身房与图书馆的开放情况，其中：

• $a_i$ 等于 $0$ 表示第 $i$ 天健身房关闭且图书馆关闭。
• $a_i$ 等于 $1$ 表示第 $i$ 天健身房关闭但图书馆开放。
• $a_i$ 等于 $2$ 表示第 $i$ 天健身房开放但图书馆关闭。
• $a_i$ 等于 $3$ 表示第 $i$ 天健身房开放且图书馆开放。

金明希望自己用来休息的天数尽可能少，但是，他一定不会 连续两天（或更多天）去健身房健身，也一定不会 连续两天（或更多天）去图书馆看书。

请你计算，金明用来休息的最少可能天数。

【输入】

第一行包含一个整数 $n$。

第二行包含 $n$ 个整数 $a_1,a_2,\dots,a_n$。

【输出】

一个整数，表示金明用来休息的最少可能天数。

【数据范围】

前 $5$ 个测试点满足 $1 \le n \le 10$。
所有测试点满足 $1 \le n \le 100$，$0 \le ai \le 3$。

【输入样例1】

4
1 3 2 0

【输出样例1】

2

【输入样例2】

7
1 3 3 2 1 2 3

【输出样例2】

0

【输入样例3】

2
2 2

【输出样例3】

1

【原题链接】

https://www.acwing.com/problem/content/4805/

---

【题目分析】

状态机 DP。

二维 DP 数组 dp[i][k] 的第一维存储天数，第二维存储 休息/去图书馆/去健身房 三种状态

• dp[i][0] 表示第 i 天休息时，前 i 天的总工作天数
• dp[i][1] 表示第 i 天去图书馆时，前 i 天的总工作天数
• dp[i][2] 表示第 i 天去健身时，前 i 天的总工作天数

具体细节见代码注释。

【复盘后的优化代码】✅

#include<bits/stdc++.h>

using namespace std;

const int N = 110;
int a[N], n;
int dp[N][5];

// 返回三个数最大值（PS: max中最多包含两个参数，所以比较三个时要写两次max）
int maxV(int x, int y, int z) {
    return max(x, max(y, z));
}

int main() {
    ios::sync_with_stdio(false);  //cin读入优化
    cin.tie(0);

    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];

    // dp[i][k] -> i表示天数，k表示状态
    // dp[i][0]表示第i天休息时，前i天的总工作天数
    // dp[i][1]表示第i天去图书馆时，前i天的总工作天数
    // dp[i][2]表示第i天去健身时，前i天的总工作天数

    for (int i = 1; i <= n; i++) {
        // 第i天选择休息（没有限制条件），取i-1天工作天数最大值
        dp[i][0] = maxV(dp[i - 1][0], dp[i - 1][1], dp[i - 1][2]);

        // 第i天选择去图书馆（必须在a[i]为1或者3的情况下），取(i-1天休息+1，i-1天去图书馆，i-1天去健身+1）最大值
        if (a[i] == 1 || a[i] == 3) dp[i][1] = maxV(dp[i - 1][0] + 1, dp[i - 1][1], dp[i - 1][2] + 1);

        // 第i天选择去健身（必须在a[i]为2或者3的情况下），取(i-1天休息+1，i-1天去图书馆+1，i-1天去健身）最大值
        if (a[i] == 2 || a[i] == 3) dp[i][2] = maxV(dp[i - 1][0] + 1, dp[i - 1][1] + 1, dp[i - 1][2]);
    }

    // PS: max中最多包含两个参数，所以比较三个时要写两次max
    cout << n - max(dp[n][0], max(dp[n][1], dp[n][2])) << endl;

    return 0;
}

【周赛现场未 AC 代码】❌

#include<bits/stdc++.h>

using namespace std;

const int N = 105;
int a[N], dp[N], n;

int main() {
    ios::sync_with_stdio(false);  //cin读入优化
    cin.tie(0);

    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];

    if (a[1] == 0) dp[1] = 0;
    else dp[1] = 1;
    for (int i = 2; i <= n; i++) {
        if (a[i] == 0) {
            dp[i] = dp[i - 1];
        } else if (a[i] == 3) {
            dp[i] = dp[i - 1] + 1;
            a[i] = 3 - a[i - 1];
        } else if (a[i] == 1) {
            if (a[i - 1] == 0 || a[i - 1] == 3 || a[i - 1] == 2) {
                dp[i] = dp[i - 1] + 1;
            } else {
                dp[i] = max(dp[i - 1], dp[i - 2] + 1);
            }
        } else {
            if (a[i - 1] == 0 || a[i - 1] == 3 || a[i - 1] == 1) {
                dp[i] = dp[i - 1] + 1;
            } else {
                dp[i] = max(dp[i - 1], dp[i - 2] + 1);
            }
        }
    }
    cout << n - dp[n] << endl;
    return 0;
}

【代码对比总结】

对比两个代码，可以发现周赛现场的代码虽然有状态分类、表示的雏形，但是由于缺乏 状态机DP 的理论知识，没能系统、完整的写出代码，存在BUG，有 4 个点未通过。

说明还是要多看课，把基础的知识点学好，再在周赛中把这些知识点融会贯通。

---