当前博客仍在更新完善中,敬请期待~
快速排序
题单 🧑🏻💻
| 题目来源 | 题目名称 | 题目链接 | 备注 | 难度 |
|---|---|---|---|---|
题解 🚀
归并排序
题目信息 📚
【题目名称】
【题目描述】
【输入】
【输出】
【输入样例】
【输出样例】
【数据范围】
【原题链接】
题目解析 🍉
【题目分析】
【C++ 代码】
OI 案例1
【题目描述】
利用快速排序算法将读入的 $N$ 个数从小到大排序后输出。
快速排序是信息学竞赛的必备算法之一。对于快速排序不是很了解的同学可以自行上网查询相关资料,掌握后独立完成。(C++ 选手请不要试图使用 STL,虽然你可以使用 sort 一遍过,但是你并没有掌握快速排序算法的精髓。)
【输入】
第 $1$ 行为一个正整数 $N$,第 $2$ 行包含 $N$ 个空格隔开的正整数 $a_i$,为你需要进行排序的数,数据保证了 $A_i$ 不超过 $10^9$。
【输出】
将给定的 $N$ 个数从小到大输出,数之间空格隔开,行末换行且无空格。
【输入样例】
5
4 2 4 5 1【输出样例】
1 2 4 4 5【数据范围】
对于 $20%$ 的数据,有 $N\leq 10^3$;
对于 $100%$ 的数据,有 $N\leq 10^5$。
【原题链接】
https://www.luogu.com.cn/problem/P1177
【题目解析】
本题如果直接提交 模版1 程序,会有 3 个超时点 ❌
因此需要优化。
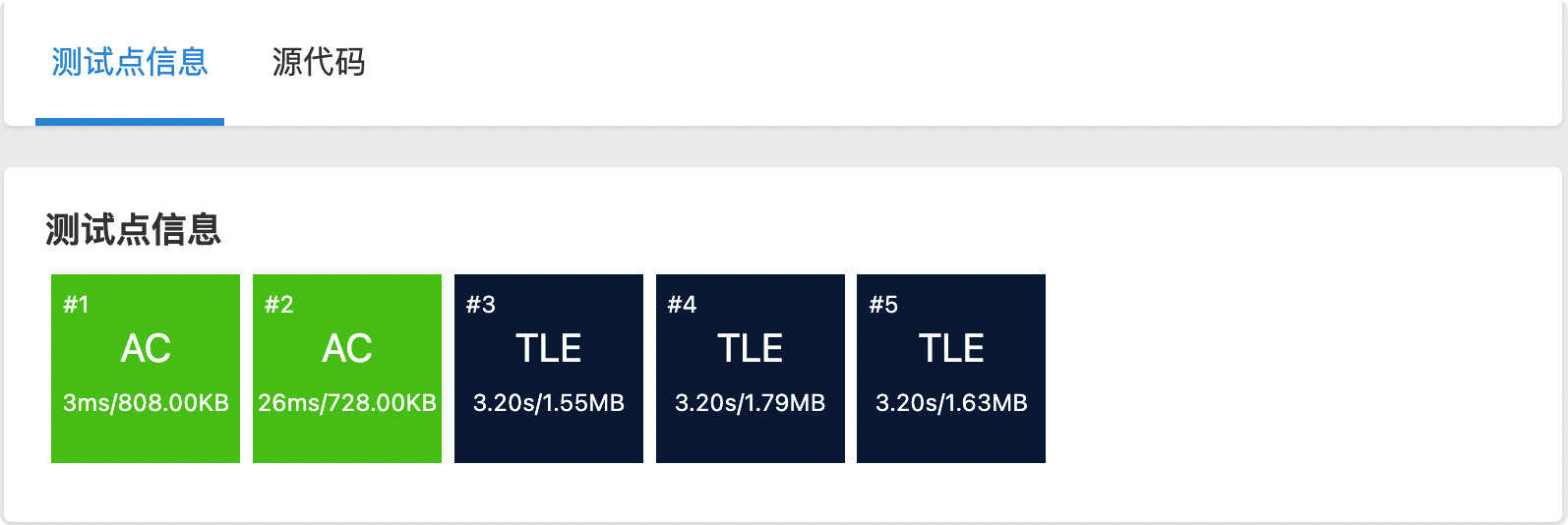
先来看一些不需要对代码算法做改进的优化。
优化方案1:将 输入输出流 改为
scanf/printf,实测该方法 失败,仍有 3 个超时点。❌优化方案2:添加优化语句,实测该方法 失败,仍有 3 个超时点(关于该优化的 相关技术博客)❌
int main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
...
}- 优化方案3:手动开启O2优化,实测该方法 失败,编译错误。(洛谷不支持手动开启 O2优化)❌
#pragma GCC optimize(2)
- 优化方法4:在洛谷 OJ 上,勾选 开启O2优化,实测该方法生效,通过所有测试点。✅
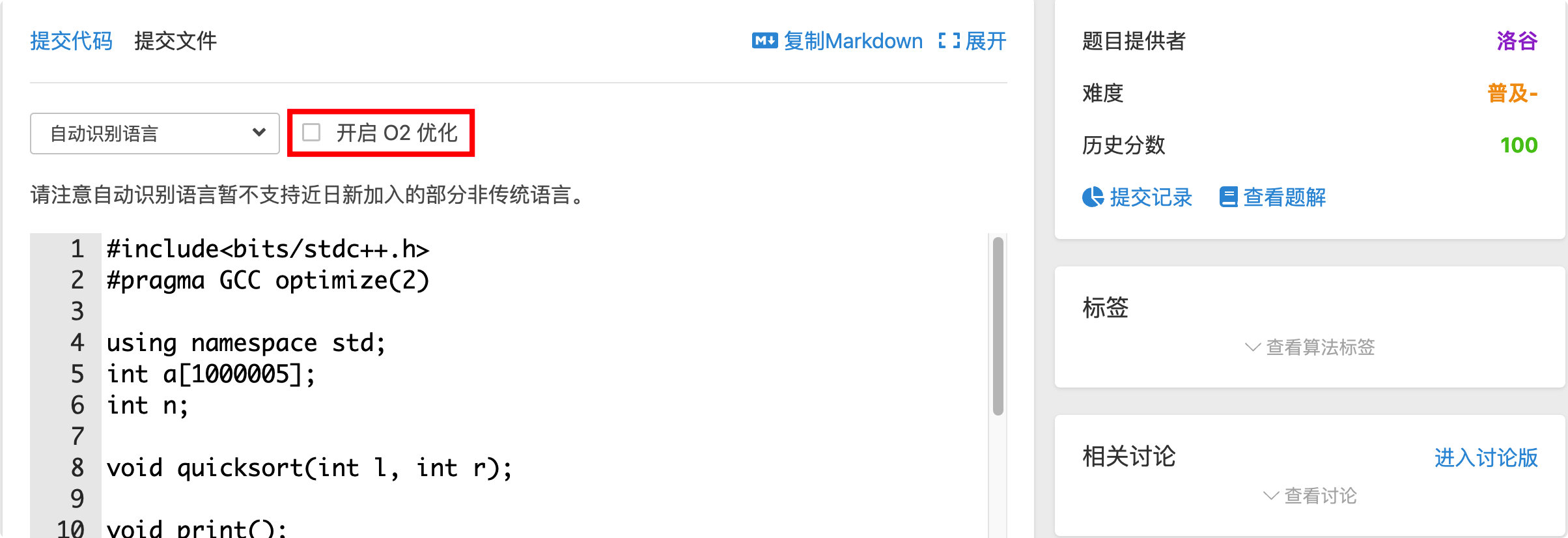

再来看一些 基于快速排序本身算法思想的优化:
首先分析 快速排序的时间复杂度:
简单来说,快速排序是一种基于二分思想的算法,时间复杂度为 $O( nlogn )$
但是,当需要排序的数组,本身就有序,或者趋近于有序时,快速排序的时间复杂度会退化成 $O(n^2)$
具体数学推导可以看下面这一篇 技术博客的分析:
基于以上对时间复杂度的分析,最终优化方案 如下:
- 优化方案1:使用
random_shuffle(a+1,a+n+1)将原数组打乱,该方案 部分奏效,但是仍有 1 个超时点。(PS:调用 1 次和调用 n 次 该代码进行打乱,最后 1 个超时点均存在)❌

- 优化方案2:使用
sort(a+1,a+n+1),直接 AC(不得不说,STL 真香)✅
#include<bits/stdc++.h>
using namespace std;
int a[1000005];
int n;
int main() {
cin >> n;
for (int i = 1; i <= n; ++i) cin >> a[i];
sort(a+1,a+n+1); //STL大法真香
for (int i = 1; i <= n; ++i) cout << a[i] << " ";
cout << endl;
return 0;
}
- 优化方案3:在传统快速排序中,我们的基准点总是选择左边界,这使得像
6 5 4 3 2 1这类数据,在递归时,quicksort(p1+1,r)失效,程序并没有「二分」,速度大大降低。
所以我们 修改基准点的选择,改为 tmp = a[(l + r) / 2] (即 模版2),成功 AC ✅
#include<bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
int n;
int a[N];
//快速排序
void qsort(int l, int r) {
//返回条件
if (l >= r) return;
//选定基准数,定义双指针
int temp = a[(l + r) >> 1];
int i = l - 1, j = r + 1;
//基本流程
while (i < j) {
do i++; while (a[i] < temp);
do j--; while (a[j] > temp);
if (i < j) swap(a[i], a[j]);
}
//递归
qsort(l, j);
qsort(j + 1, r);
}
int main() {
ios::sync_with_stdio(false); //cin读入优化
cin.tie(0);
//读入数据
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> a[i];
}
//快速排序
qsort(1, n);
//输出结果
for (int i = 1; i <= n; i++) {
cout << a[i] << " ";
}
cout << endl;
return 0;
}



