并查集
题单 🧑🏻💻
| 题目来源 | 题目名称 | 题目链接 | 备注 | 难度 |
|---|---|---|---|---|
| HDU - 1856 | More is better | 链接🔗 | 并查集求集合元素数量最大值 | 🟢 |
| 蓝桥杯 2017 国 C | 合根植物 | 链接🔗 | 并查集求集合数量 | 🟢 |
题解 🚀
More is better
题目信息 📚
【题目名称】HDU P1856 - More is better
【题目描述】
Mr Wang wants some boys to help him with a project. Because the project is rather complex, the more boys come, the better it will be. Of course there are certain requirements.
Mr Wang selected a room big enough to hold the boys. The boy who are not been chosen has to leave the room immediately. There are 100000 boys in the room numbered from $1$ to $100000$ at the very beginning. After Mr Wang’s selection any two of them who are still in this room should be friends (direct or indirect), or there is only one boy left. Given all the direct friend-pairs, you should decide the best way.
【输入】
The first line of the input contains an integer $n (0 \le n \le 100 000)$ - the number of direct friend-pairs.
The following n lines each contains a pair of numbers $A$ and $B$ separated by a single space that suggests $A$ and $B$ are direct friends. $
【输出】
The output in one line contains exactly one integer equals to the maximum number of boys Mr Wang may keep.
【输入样例】
4
1 2
3 4
5 6
1 6
4
1 2
3 4
5 6
7 8【输出样例】
4
2【原题链接】
https://vjudge.net/problem/HDU-1856
题目解析 🍉
【题目分析】
并查集基础题
方法一:在原始模版(pre[] 数组 + find() 函数 + join() 函数)的基础上,添加 cnt[] 数组纪录当前集合的元素总数(主要难点在于 cnt[] 数组的添加位置,以及是否每个元素都需要记录 cnt 的值,还是只需要代表元记录即可)。
【C++ 代码】
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
int pre[N], cnt[N], n, a, b;
// 并查集初始化
void init() {
for (int i = 1; i < N; i++) {
pre[i] = i;
cnt[i] = 1;
}
}
// 查找编号为x的元素所在集合
int find(int x) {
if (x != pre[x]) pre[x] = find(pre[x]);
return pre[x];
}
// 合并两个集合
void join(int a, int b) {
int xa = find(a);
int xb = find(b);
if (xa != xb) {
pre[xa] = xb;
cnt[xb] += cnt[xa];
}
}
int main() {
ios::sync_with_stdio(false); //cin读入优化
cin.tie(0);
while (cin >> n) {
init(); // 并查集初始化
for (int i = 1; i <= n; i++) {
cin >> a >> b;
join(a, b); // 合并
}
// 输出集合元素数量最大值
int res = 0;
for (int i = 1; i < N; i++) res = max(res, cnt[i]);
cout << res << endl;
}
return 0;
}方法二:保持原始模版(pre[] 数组 + find() 函数 + join() 函数)不变的基础上,使用 unordered_map<int, vector<int>> 来存储所有集合。
# include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int pre[N], n, a, b;
// 并查集初始化
void init() {
for (int i = 1; i < N; i++) {
pre[i] = i;
}
}
// 查找编号为x的元素所在集合
int find(int x) {
if (x != pre[x]) pre[x] = find(pre[x]);
return pre[x];
}
// 合并两个集合
void join(int x, int y) {
int i = find(x);
int j = find(y);
if (i != j) {
pre[i] = j;
}
}
int main() {
ios::sync_with_stdio(false); //cin读入优化
cin.tie(0);
while (cin >> n) {
init();
for (int i = 1; i <= n; i++) {
cin >> a >> b;
join(a, b);
}
// 存储当前已有的集合至sets中
unordered_map<int, vector<int>> sets;
for (int i = 1; i < N; i++) {
int root = find(i);
sets[root].push_back(i);
}
// 比较当前所有集合元素数量的最大值
int maxV = -1;
for (const auto &p: sets) { // 思考代码const auto &p 与 auto p, auto &p 的区别
maxV = max(maxV,int(p.second.size()));
}
cout << maxV << endl;
}
return 0;
}合根植物
题目信息 📚
【题目名称】合根植物
【题目描述】
w 星球的一个种植园,被分成 $m \times n$ 个小格子(东西方向 $m$ 行,南北方向 $n$ 列)。每个格子里种了一株合根植物。
这种植物有个特点,它的根可能会沿着南北或东西方向伸展,从而与另一个格子的植物合成为一体。
如果我们告诉你哪些小格子间出现了连根现象,你能说出这个园中一共有多少株合根植物吗?
【输入格式】
第一行,两个整数 $m$,$n$,用空格分开,表示格子的行数、列数($1<m,n<1000$)。
接下来一行,一个整数 $k$,表示下面还有 $k$ 行数据 $(0<k<10^5)$。
接下来 $k$ 行,每行两个整数 $a$,$b$,表示编号为 $a$ 的小格子和编号为 $b$ 的小格子合根了。
格子的编号一行一行,从上到下,从左到右编号。
比如:$5 \times 4$ 的小格子,编号:
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
17 18 19 20【输出格式】
一行一个整数,表示答案
【输入样例 #1】
5 4
16
2 3
1 5
5 9
4 8
7 8
9 10
10 11
11 12
10 14
12 16
14 18
17 18
15 19
19 20
9 13
13 17【输出样例 #1】
5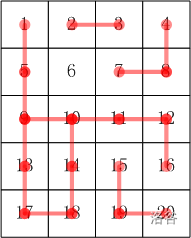
【题目链接】
https://www.luogu.com.cn/problem/P8654?contestId=159847
题目解析 🍉
【题目分析】
并查集基础题(表面上套了一个二维的壳,实际就是一维)
方法一:利用 unordered_map 存储集合并进行统计。
# include<bits/stdc++.h>
using namespace std;
const int N = 1e3 + 5;
int pre[N * N], m, n, k;
void init(int num) {
for (int i = 1; i <= num; i++) {
pre[i] = i;
}
}
int find(int x) {
if (pre[x] != x) pre[x] = find(pre[x]);
return pre[x];
}
void join(int x, int y) {
int i = find(x);
int j = find(y);
if (i != j) pre[i] = j;
}
int main() {
cin >> m >> n >> k;
init(m * n);
int a, b;
for (int i = 1; i <= k; i++) {
cin >> a >> b;
join(a, b);
}
// 存储当前所有集合
unordered_map<int, int> sets;
for (int i = 1; i <= n*m; i++) {
int root = find(i);
sets[root]++;
}
// 输出集合数量
cout << sets.size() << endl;
return 0;
}方法二:利用代表元的 pre[i] = i 的特性统计数量。
# include<bits/stdc++.h>
using namespace std;
const int N = 1e3 + 5;
int pre[N * N], m, n, k;
void init(int num) {
for (int i = 1; i <= num; i++) {
pre[i] = i;
}
}
int find(int x) {
if (pre[x] != x) pre[x] = find(pre[x]);
return pre[x];
}
void join(int x, int y) {
int i = find(x);
int j = find(y);
if (i != j) pre[i] = j;
}
int main() {
cin >> m >> n >> k;
init(m * n);
int a, b;
for (int i = 1; i <= k; i++) {
cin >> a >> b;
join(a, b);
}
// 利用代表元的特性,统计集合数量
int cnt = 0;
for (int i = 1; i <= m * n; i++) {
if (pre[i] == i) cnt++;
}
cout << cnt << endl;
return 0;
}方法三:利用 每次合并,集合总数-1 的性质求解
# include<bits/stdc++.h>
using namespace std;
const int N = 1e3 + 5;
int pre[N * N], m, n, k;
int cnt; // 集合总数
void init(int num) {
for (int i = 1; i <= num; i++) pre[i] = i;
}
int find(int x) {
if (pre[x] != x) pre[x] = find(pre[x]);
return pre[x];
}
void join(int x, int y) {
int i = find(x);
int j = find(y);
if (i != j) {
pre[i] = j;
cnt--; // 每次合并时,集合总数-1
}
}
int main() {
cin >> m >> n >> k;
cnt = m * n; // 初始集合总数
init(m * n);
int a, b;
for (int i = 1; i <= k; i++) {
cin >> a >> b;
join(a, b);
}
cout << cnt << endl;
return 0;
}


