复盘｜2023多校新生周赛十

信息奥赛复盘｜2023多校新生周赛十（2023.11.25）

比赛信息 📚

时间：2023 年 11 月 25 日 18:00 - 21:00

竞赛链接：（仅ZJNU内网登录）

ACM集训队讲解视频：/

个人情况 ✍️

本周个人排名：12/13

AC情况：1/6

比赛时间：2023.11.25（18：00 - 21:00）

忘记周赛时间了，进场的时候已经只剩下25min了，只AC了B题，接近做出A题。

题目列表 🧑🏻‍💻

题目名称	难度
T1 - Divide it!	🟡
T2 - Merge it!	🟢
T3 - Lose it!	🟡
T4 - Recover it!	🟡
T5 - Cover it!	🟡
T6 - Destroy it!	🟡

---

题解 🚀

A - Divide it!

题目信息 📚

【题目描述】

You are given an integer $n$.

You can perform any of the following operations with this number an arbitrary (possibly, zero) number of times:

1. Replace $n$ with $\frac{n}{2}$ if $n$ is divisible by $2$;
2. Replace $n$ with $\frac{2n}{3}$ if $n$ is divisible by $3$;
3. Replace $n$ with $\frac{4n}{5}$ if $n$ is divisible by $5$.

For example, you can replace $30$ with $15$ using the first operation, with $20$ using the second operation or with $24$ using the third operation.

Your task is to find the minimum number of moves required to obtain $1$ from $n$ or say that it is impossible to do it.

You have to answer $q$ independent queries.

【输入】

The first line of the input contains one integer $q$ ($1 \le q \le 1000$) — the number of queries.

The next $q$ lines contain the queries. For each query you are given the integer number $n$ ($1 \le n \le 10^{18}$).

【输出】

Print the answer for each query on a new line. If it is impossible to obtain $1$ from $n$, print -1. Otherwise, print the minimum number of moves required to do it.

【输入样例1】

7
1
10
25
30
14
27
1000000000000000000

【输出样例1】

0
4
6
6
-1
6
72

【题目来源】

https://codeforces.com/problemset/problem/1176/A

---

题目解析 🍉

【题目分析】

签到题，简单贪心 + 模拟即可。（可以选择 「迭代」或者「递归」实现）

【C++代码】迭代法 ✅

#include<bits/stdc++.h>

using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
LL n, cnt;

void solve() {
    cin >> n;
    cnt = 0;
    // 迭代求解
    while (n > 1) {
        if (n % 2 == 0) {
            cnt++, n /= 2;
        } else if (n % 3 == 0) {
            cnt++, n = n * 2 / 3;
        } else if (n % 5 == 0) {
            cnt++, n = n * 4 / 5;
        } else {
            cnt = -1;
            break;
        }
    }
    cout << cnt << endl;
}

int main() {
    ios::sync_with_stdio(false);  //cin读入优化
    cin.tie(0);

    int _ = 1;
    cin >> _;
    while (_--) {
        solve();
    }

    return 0;
}

【C++代码】递归法 ✅

#include<bits/stdc++.h>

using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
LL n, cnt;

LL f(LL n) {
    if (n == 1) return 0;
    else if (n % 2 == 0) return 1 + f(n / 2);
    else if (n % 3 == 0) return 1 + f(n * 2 / 3);
    else if (n % 5 == 0) return 1 + f(n * 4 / 5);
    else return -0x3f3f3f3f;
}

void solve() {
    cin >> n;
    LL cnt = f(n);
    if (cnt >= 0) cout << cnt << endl;
    else cout << -1 << endl;
}

int main() {
    ios::sync_with_stdio(false);  //cin读入优化
    cin.tie(0);

    int _ = 1;
    cin >> _;
    while (_--) {
        solve();
    }

    return 0;
}

---

B - Merge it!

题目信息 📚

【题目描述】

You are given an array $a$ consisting of $n$ integers $a_1, a_2, \dots , a_n$.

In one operation you can choose two elements of the array and replace them with the element equal to their sum (it does not matter where you insert the new element). For example, from the array $[2, 1, 4]$ you can obtain the following arrays: $[3, 4]$, $[1, 6]$ and $[2, 5]$.

Your task is to find the maximum possible number of elements divisible by $3$ that are in the array after performing this operation an arbitrary (possibly, zero) number of times.

You have to answer $t$ independent queries.

【输入】

The first line contains one integer $t$ ($1 \le t \le 1000$) — the number of queries.

The first line of each query contains one integer $n$ ($1 \le n \le 100$).

The second line of each query contains $n$ integers $a_1, a_2, \dots , a_n$ ($1 \le a_i \le 10^9$).

【输出】

For each query print one integer in a single line — the maximum possible number of elements divisible by $3$ that are in the array after performing described operation an arbitrary (possibly, zero) number of times.

【输入样例1】

2
5
3 1 2 3 1
7
1 1 1 1 1 2 2

【输出样例1】

3
3

【提示】

In the first query of the example you can apply the following sequence of operations to obtain $3$ elements divisible by $3$: $[3, 1, 2, 3, 1] \rightarrow [3, 3, 3, 1]$.

In the second query you can obtain $3$ elements divisible by $3$ with the following sequence of operations: $[1, 1, 1, 1, 1, 2, 2] \rightarrow [1, 1, 1, 1, 2, 3] \rightarrow [1, 1, 1, 3, 3] \rightarrow [2, 1, 3, 3] \rightarrow [3, 3, 3]$.

【题目来源】

https://codeforces.com/problemset/problem/1176/B

---

题目解析 🍉

【题目分析】

数学 + 思维

只要分析出「3的倍数不用合并，如何合并余数为1、2的数」即可。

【C++代码】✅

#include<bits/stdc++.h>

using namespace std;
typedef long long LL;
const int N = 110;
int n, a[N];

void solve() {
    // map统计余数为0，1，2数量
    map<int, int> mp;
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
        mp[a[i] % 3]++;
    }

    // 余数为0，自然是3的倍数，无需合并
    int cnt = mp[0];
    // 余数为1、2，需要进行合并
    int t = min(mp[1], mp[2]);
    // 合并后多出来的部分，也需要内部合并
    cnt += t + (mp[1] - t) / 3 + (mp[2] - t) / 3;
    cout << cnt << endl;
}

int main() {
    ios::sync_with_stdio(false);  //cin读入优化
    cin.tie(0);

    int _ = 1;
    cin >> _;
    while (_--) {
        solve();
    }

    return 0;
}

---

C - Lose it!

题目信息 📚

【题目描述】

You are given an array $a$ consisting of $n$ integers. Each $a_i$ is one of the six following numbers: $4, 8, 15, 16, 23, 42$.

Your task is to remove the minimum number of elements to make this array good.

An array of length $k$ is called good if $k$ is divisible by $6$ and it is possible to split it into $\frac{k}{6}$ subsequences $4, 8, 15, 16, 23, 42$.

Examples of good arrays:

• $[4, 8, 15, 16, 23, 42]$ (the whole array is a required sequence);
• $[4, 8, 4, 15, 16, 8, 23, 15, 16, 42, 23, 42]$ (the first sequence is formed from first, second, fourth, fifth, seventh and tenth elements and the second one is formed from remaining elements);
• $[]$ (the empty array is good).

Examples of bad arrays:

• $[4, 8, 15, 16, 42, 23]$ (the order of elements should be exactly $4, 8, 15, 16, 23, 42$);
• $[4, 8, 15, 16, 23, 42, 4]$ (the length of the array is not divisible by $6$);
• $[4, 8, 15, 16, 23, 42, 4, 8, 15, 16, 23, 23]$ (the first sequence can be formed from first six elements but the remaining array cannot form the required sequence).

【输入】

The first line of the input contains one integer $n$ ($1 \le n \le 5 \cdot 10^5$) — the number of elements in $a$.

The second line of the input contains $n$ integers $a_1, a_2, \dots, a_n$ (each $a_i$ is one of the following numbers: $4, 8, 15, 16, 23, 42$), where $a_i$ is the $i$-th element of $a$.

【输出】

Print one integer — the minimum number of elements you have to remove to obtain a good array.

【输入样例1】

5
4 8 15 16 23

【输出样例1】

5

【输入样例2】

12
4 8 4 15 16 8 23 15 16 42 23 42

【输出样例2】

0

【输入样例3】

15
4 8 4 8 15 16 8 16 23 15 16 4 42 23 42

【输出样例3】

3

【题目来源】

https://codeforces.com/problemset/problem/1176/C

---

题目解析 🍉

【题目分析】

思维 + 统计

【C++代码】✅

#include<bits/stdc++.h>

using namespace std;
typedef long long LL;
const int N = 5e5 + 10;
int a[N], n;
map<int, int> mp;

// 查找离散化下标
int findi(int x) {
    int t[6] = {4, 8, 15, 16, 23, 42};
    return lower_bound(t, t + 6, x) - t + 1;
}

int main() {
    ios::sync_with_stdio(false);  //cin读入优化
    cin.tie(0);

    cin >> n;
    for (int i = 1; i <= n; i++) {
        // 逐个读入元素
        cin >> a[i];
        int id = findi(a[i]);
        mp[id]++;

        // 判断当前元素，是否有合法个前置元素
        // 如当前读到15，且map[findi(15)]=3，说明共有3个15
        // 则前面至少有3个4和8，该15才合法
        for (int i = 1; i < id; i++) {
            if (mp[i] < mp[id]) {
                mp[id]--;
                break;
            }
        }
    }

    // 输出答案
    int cnt = 0x3f3f3f3f;
    for (int i = 1; i <= 6; i++) {
        cnt = min(cnt, mp[i]);
    }
    cout << n - cnt * 6 << endl;

    return 0;
}

---

D - Recover it!

题目信息 📚

【题目描述】

Authors guessed an array $a$ consisting of $n$ integers; each integer is not less than $2$ and not greater than $2 \cdot 10^5$. You don’t know the array $a$, but you know the array $b$ which is formed from it with the following sequence of operations:

1. Firstly, let the array $b$ be equal to the array $a$;
2. Secondly, for each $i$ from $1$ to $n$:
   • if $a_i$ is a prime number, then one integer $p_{a_i}$ is appended to array $b$, where $p$ is an infinite sequence of prime numbers ($2, 3, 5, \dots$);
   • otherwise (if $a_i$ is not a prime number), the greatest divisor of $a_i$ which is not equal to $a_i$ is appended to $b$;
3. Then the obtained array of length $2n$ is shuffled and given to you in the input.

Here $p_{a_i}$ means the $a_i$-th prime number. The first prime $p_1 = 2$, the second one is $p_2 = 3$, and so on.

Your task is to recover any suitable array $a$ that forms the given array $b$. It is guaranteed that the answer exists (so the array $b$ is obtained from some suitable array $a$). If there are multiple answers, you can print any.

【输入】

The first line of the input contains one integer $n$ ($1 \le n \le 2 \cdot 10^5$) — the number of elements in $a$.

The second line of the input contains $2n$ integers $b_1, b_2, \dots, b_{2n}$ ($2 \le b_i \le 2750131$), where $b_i$ is the $i$-th element of $b$. $2750131$ is the $199999$-th prime number.

【输出】

In the only line of the output print $n$ integers $a_1, a_2, \dots, a_n$ ($2 \le a_i \le 2 \cdot 10^5$) in any order — the array $a$ from which the array $b$ can be obtained using the sequence of moves given in the problem statement. If there are multiple answers, you can print any.

【输入样例1】

3
3 5 2 3 2 4

【输出样例1】

3 4 2

【输入样例2】

1
2750131 199999

【输出样例2】

199999

【输入样例3】

1
3 6

【输出样例3】

6

【题目来源】

https://codeforces.com/problemset/problem/1176/D

---

题目解析 🍉

【题目分析】

线性筛 + 求最大因子 + 桶思想计数

【C++代码】

#include<bits/stdc++.h>

using namespace std;
typedef long long LL;
const int N = 2e5 + 10;  // a数组最大个数
const int P = 3e6 + 10;  // 最大质数的范围
int book[P]; // 线性筛标记数组
vector<int> p; // 存储1～P所有的质数
int prime[P];  // prime[i]表示质数i对应的下标，如prime[2]=1,prime[5]=3
LL divisor[P];  // div[i]存储i的最大divisor

int n, b[N * 2];  // 读入b数组
int br[P];  // 桶数组，标记b数组中每个数出现几次
vector<int> a; // 存储原数组

// 线性筛，在O(N)的时间内筛选出1~N的质数，存入vector p中
// 在线性筛的基础上，求出P以内每个数的最大divisor（质数为1，合数为自身/最大质因子）
void sieve() {
    for (int i = 2; i < P; i++) {
        if (book[i] == 0) {
            // 当前i为质数
            p.push_back(i);  // 加入p中
            divisor[i] = 1;  // 质数的最大divisor为1
        } else {
            // 当前i为合数，统计其最大质因子
            // 思考为什么这一步不集成在线性筛中
            for (int j = 2; j <= i / j; j++) {
                if (i % j == 0) {
                    divisor[i] = i / j;
                    break;
                }
            }
        }
        // 线性筛
        for (int j = 0; j < p.size() && i * p[j] < P; j++) {
            book[i * p[j]] = 1;
            if (i % p[j] == 0) {
                break;
            }
        }
    }
    // 计算prime数组
    for (int i = 0; i < p.size(); i++) {
        prime[p[i]] = i + 1;
    }
}

int main() {
    ios::sync_with_stdio(false);  //cin读入优化
    cin.tie(0);

    // 读入b数组，并标记
    cin >> n;
    for (int i = 1; i <= 2 * n; i++) {
        cin >> b[i];
        br[b[i]]++;
    }

    // 线性筛预处理
    sieve();

    // 对b数组进行排序
    sort(b + 1, b + 2 * n + 1);

    // 从大到小，逐个处理
    for (int i = 2 * n; i > 0; i--) {
//        cout << b[i] << "   ";
        if (divisor[b[i]] > 1 && br[b[i]] && br[divisor[b[i]]]) {
            // 当前数字为合数
            br[b[i]]--;
            br[divisor[b[i]]]--;
            a.push_back(b[i]);
        } else if (divisor[b[i]] == 1 && br[b[i]] && br[prime[b[i]]]) {
            // 当前数字为质数
            br[b[i]]--;
            br[prime[b[i]]]--;
            a.push_back(prime[b[i]]);
        }
    }

    // 输出a数组
    for (int i = 0; i < a.size(); i++) {
        cout << a[i] << " ";
    }
    cout << endl;

    return 0;
}

---

E - Cover it!

题目信息 📚

【题目描述】

You are given an undirected unweighted connected graph consisting of $n$ vertices and $m$ edges. It is guaranteed that there are no self-loops or multiple edges in the given graph.

Your task is to choose at most $\lfloor\frac{n}{2}\rfloor$ vertices in this graph so each unchosen vertex is adjacent (in other words, connected by an edge) to at least one of chosen vertices.

It is guaranteed that the answer exists. If there are multiple answers, you can print any.

You will be given multiple independent queries to answer.

【输入】

The first line contains a single integer $t$ ($1 \le t \le 2 \cdot 10^5$) — the number of queries.

Then $t$ queries follow.

The first line of each query contains two integers $n$ and $m$ ($2 \le n \le 2 \cdot 10^5$, $n - 1 \le m \le min(2 \cdot 10^5, \frac{n(n-1)}{2})$) — the number of vertices and the number of edges, respectively.

The following $m$ lines denote edges: edge $i$ is represented by a pair of integers $v_i$, $u_i$ ($1 \le v_i, u_i \le n$, $u_i \ne v_i$), which are the indices of vertices connected by the edge.

There are no self-loops or multiple edges in the given graph, i. e. for each pair ($v_i, u_i$) there are no other pairs ($v_i, u_i$) or ($u_i, v_i$) in the list of edges, and for each pair ($v_i, u_i$) the condition $v_i \ne u_i$ is satisfied. It is guaranteed that the given graph is connected.

It is guaranteed that $\sum m \le 2 \cdot 10^5$ over all queries.

【输出】

For each query print two lines.

In the first line print $k$ ($1 \le \lfloor\frac{n}{2}\rfloor$) — the number of chosen vertices.

In the second line print $k$ distinct integers $c_1, c_2, \dots, c_k$ in any order, where $c_i$ is the index of the $i$-th chosen vertex.

It is guaranteed that the answer exists. If there are multiple answers, you can print any.

【数据范围】

• All values in input are integers.
• $1 \leq N \leq 200000$
• $1 \leq a_i \leq N$

【输入样例1】

2
4 6
1 2
1 3
1 4
2 3
2 4
3 4
6 8
2 5
5 4
4 3
4 1
1 3
2 3
2 6
5 6

【输出样例1】

2
1 3
3
4 3 6

【提示】

In the first query any vertex or any pair of vertices will suffice.

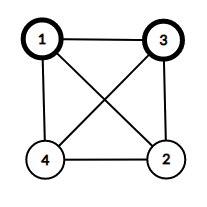
Note that you don’t have to minimize the number of chosen vertices. In the second query two vertices can be enough (vertices $2$ and $4$) but three is also ok.

【题目来源】

---

题目解析 🍉

【C++代码】✅

---

F - Destroy it!

题目信息 📚

【题目描述】

You are playing a computer card game called Splay the Sire. Currently you are struggling to defeat the final boss of the game.

The boss battle consists of $n$ turns. During each turn, you will get several cards. Each card has two parameters: its cost $c_i$ and damage $d_i$. You may play some of your cards during each turn in some sequence (you choose the cards and the exact order they are played), as long as the total cost of the cards you play during the turn does not exceed $3$. After playing some (possibly zero) cards, you end your turn, and all cards you didn’t play are discarded. Note that you can use each card at most once.

Your character has also found an artifact that boosts the damage of some of your actions: every $10$-th card you play deals double damage.

What is the maximum possible damage you can deal during $n$ turns?

【输入】

The first line contains one integer $n$ ($1 \le n \le 2 \cdot 10^5$) — the number of turns.

Then $n$ blocks of input follow, the $i$-th block representing the cards you get during the $i$-th turn.

Each block begins with a line containing one integer $k_i$ ($1 \le k_i \le 2 \cdot 10^5$) — the number of cards you get during $i$-th turn. Then $k_i$ lines follow, each containing two integers $c_j$ and $d_j$ ($1 \le c_j \le 3$, $1 \le d_j \le 10^9$) — the parameters of the corresponding card.

It is guaranteed that $\sum \limits_{i = 1}^{n} k_i \le 2 \cdot 10^5$.

【输出】

Print one integer — the maximum damage you may deal.

【输入样例1】

5
3
1 6
1 7
1 5
2
1 4
1 3
3
1 10
3 5
2 3
3
1 15
2 4
1 10
1
1 100

【输出样例1】

263

【提示】

In the example test the best course of action is as follows:

During the first turn, play all three cards in any order and deal $18$ damage.

During the second turn, play both cards and deal $7$ damage.

During the third turn, play the first and the third card and deal $13$ damage.

During the fourth turn, play the first and the third card and deal $25$ damage.

During the fifth turn, play the only card, which will deal double damage ($200$).

【题目来源】

---

题目解析 🍉

【题目分析】

【C++代码】

---